 |
ジオメトリ設定を一般化した水中Structure-from-Motionの研究 |
|
近年, ロボットビジョン・海洋生物学・スポーツ科学等の分野において水中3次元復元の需要が高まっている.
水中3次元復元の有力な手法の一つとしてStructure-from-Motion (SfM)が知られており, 水面において光の屈折が発生することを考慮した非中心射影モデルを用いる必要があるという点で注目を集めている.
一方で, 水中SfMの研究はカメラの前に正対した状態で平らなハウジング境界面が固定されるというジオメトリを前提としたものに偏っており, ハウジング境界面が動くケースやハウジング境界面が平らでないケース(波立つ水面など)を想定した研究はあまり行われていなかった(表1). 
一般化水中SfMモデル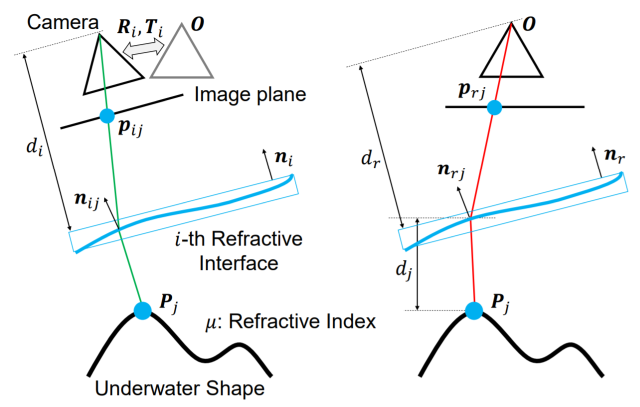
表1における各シナリオは全てこのモデルの特殊化事例として表現できる. 例えば, カメラと屈折境界面間の距離を一定とし, 屈折境界面の法線を全てカメラに正対とすると一般的な水中SfMのジオメトリ設定と同値となる. 最適化アルゴリズムバンドル調整などの3次元復元における最適化アルゴリズムには通常順投影による再投影誤差最小化が用いられる. しかし, 本モデルにおいては屈折境界面が位置ごとに異なる(連続性を仮定していない)法線を持つため, 順投影計算を解析的に行えない. そこで, 画像上の各点から3次元空間中に対してレイを飛ばし, ある一点でレイ同士が交差することを拘束とする.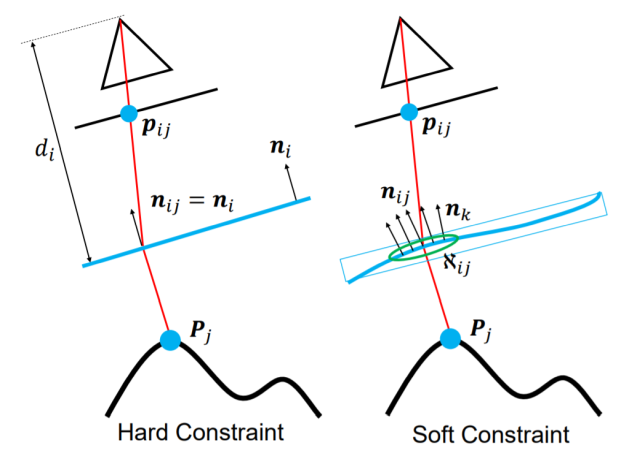
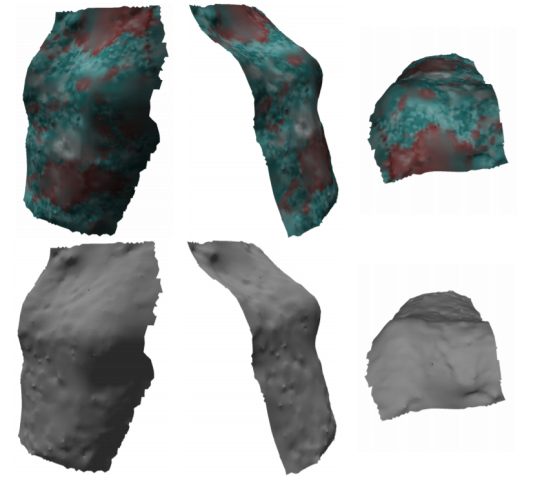
水中SfM実測結果以下に本研究の一般化水中SfMモデルと最適化アルゴリズムによる復元結果を示す.


Publications
|
| Kawasaki Laboratory |